Page 9 - ePD11108_數學A跨越講義_課本PDF
P. 9
ٜᇞ˙ό ୋ 1
ᕚ ˴
1 c
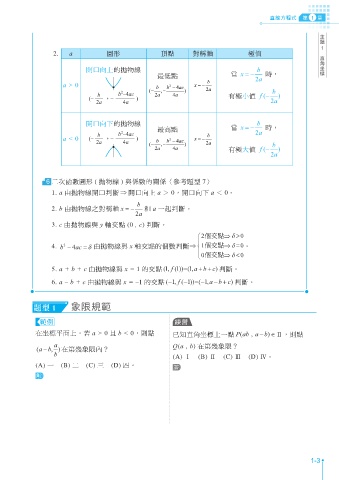
2. a 圖形 頂點 對稱軸 極值 ᅺ ٜ ԉ Ѭ
開口向上的拋物線 b
最低點 當 x =− 時,
b 2 a
a > 0 b b − 4ac x = −
2
( − ,− ) 2a b
2a 4a 有極小值 f (− )
2 a
開口向下的拋物線 b
最高點 當 x =− 2 a 時,
b
a < 0 b b − 4ac x = −
2
( − ,− ) 2a b
2a 4a 有極大值 f (− )
2 a
6 二次函數圖形 ( 拋物線 ) 與係數的關係〈參考題型 7〉
1. a 由拋物線開口判斷 ⇒ 開口向上 a > 0,開口向下 a < 0。
b
2. b 由拋物線之對稱軸 x =− 和 a 一起判斷。
2 a
3. c 由拋物線與 y 軸交點 (0 , c) 判斷。
δ
2↚″灭 ⇒ ˑʳ0
δ
2
4. b − 4 ac = δ 由拋物線與 x 軸交點的個數判斷⇒ 1↚″灭 ⇒ ːʳ0。
δ
0↚″灭 ⇒ ˏʳ0
++
5. a + b + c 由拋物線與 x = 1 的交點 (, ())( ,1 f 1 = 1 abc ) 判斷。
6. a – b + c 由拋物線與 x = –1 的交點 (, ())( ,−1 f −1 = −1 a − +bc ) 判斷。
ᕚۨ 1 ࠢᇍ
ᇍԷ ᇖ୦
在坐標平面上,若 a > 0 且 b < 0,則點 已知直角坐標上一點 Paba b( , − )∈Ⅱ,則點
a Q(a , b) 在第幾象限?
−
(ab , ) 在第幾象限內?
b (A) Ⅰ (B) Ⅱ (C) Ⅲ (D) Ⅳ。
(A) 一 (B) 二 (C) 三 (D) 四。 ഈ
༆
1-3
1% @DI @ JOEE ɪʹ