Page 25 - ePD701_商職數學B影視版金箍棒_課本PDF

1 Chapter

直線方程式

主題三 函數圖形

1. בᇴؠཌྷĈ

對於每一個 x 值(自變數)已知時，就有一個且只有一個 y 值(應變數)與之對應，

這就是函數的觀念。

1 老師講解 1 學生練習

 2x  5 , x  8  x  2 2 , x  2
設 ()  fx  x  2 x ,  8  x  8， 設 ()   3x  5 ,  1 x   2，
fx


 
 x  4 , x   8  6 , x  1

f
試求下列各式之值。 試求 (3)  f (1)  f ( 1)之值。

(1) (3) (2) (12)f (3) ( 8) (4) ( (5))
f
ff
f
解
【代碼】a61a01m2
解

2 老師講解 2 學生練習

x 3
已知函數 ( f )  2x  5，求 () 之值。
f
x
) 5
f
f
x
x  1 4 設 ( 2  ) 1  2  5，則求 ( 之值。
解 【代碼】a61a01m3
解

2. ቢݭבᇴĈ


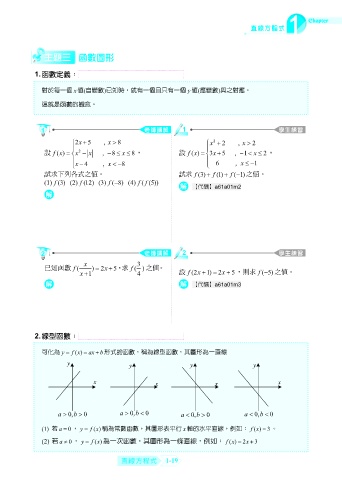
可化為  y ()  f x ax b 形式的函數，稱為線型函數，其圖形為一直線
y y y y

x x x x

a  0,b  0 a  0,b  0 a  0,b  0 a  0,b  0


fx
x
(1) 若 a 0 ， y f () 稱為常數函數，其圖形表平行 x 軸的水平直線，例如： () 3 。

0
3
(2) 若  ，  f () 為一次函數，其圖形為一條直線，例如： () 2 
a
fx
x
x
y
直線方程式 1-19