Page 11 - AD02307_數位邏輯含實習升學寶典

俪∴塄∡

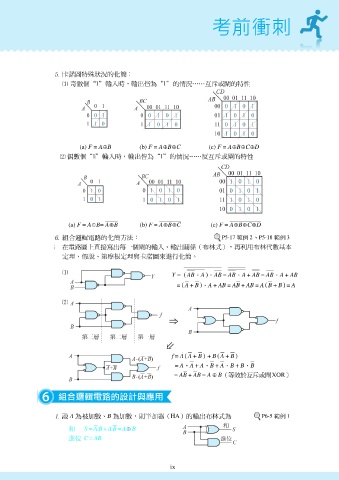
卡諾圖 特 殊狀況 的化簡：
奇 數個“ 1 ”輸入時，輸出皆為“ 1 ”的 情況… 斥 或 的特性
互閘
…

(a) F = A B (b) F = A B C (c) F = A B C D

斥閘
…
偶 數個“ 1 ”輸入時，輸出皆為“ 1 ”的 情況… 反互 或 的特性

(a) F = A B= A B (b) F = A B C (c) F = A B C D
P5-17 2 、P5-18 3
組合邏輯電路的化簡方法： 範例 範例

關係
閘的輸入、輸出
在電路
圖上直接寫出每一個
定 理 、 假說 、第 摩根 定 理 與 卡諾圖 來進行化簡。 （ 布林 式），再 利 用 布林 代數基 本
Y= AB ．A ．AB = AB ．A+ AB = AB ．A+ AB
= A+ B ．A+ AB= AB+AB =A B+B =A

f= A A+ B +B A+ B

=A ．A+ A ．B+ A ．B+B ．B
=AB+ AB = A
斥 B （等效於互 或閘XOR ）
6 ಢӫᡒᒮႫၯޟ೩ॎᇄᔖҢ

設 A 為 被 加數、 B 為加數，則 半 加器（ HA ）的輸出 布林 式為 P6-5 範例 1

S = AB + A B = A B
和
C = AB
進位