Page 12 - AD02307_數位邏輯含實習升學寶典

俪∴塄∡

設 A 為 被 加數、 B 為加數而 C i 為前一 級 加法器的進位，則 加器（ FA ）的輸出 全布
P6-6 2
林 式為 範例
S o = A B
和 C i
C o = AB + BC i + AC i = AB + C i A B
進位
設 A 為 被 減數、 B 為減數，則 半 減器（ HS ）的輸出 布林 式為 P6-9 範例 3

D o = AB + A B = A B
差
位 B o = AB
借

設 A 為 被 減數、 B 為減數而 B i 為前一 減法器的 級 位，則 借減器（ FS ）的輸出 布
全
P6-11 4
林 式為 範例
D o = A B
差 B i
位 B o A , B , B i = AB + AB i + BB i = AB + B i A B
借
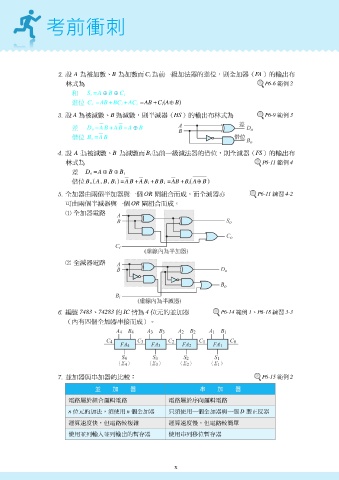
OR 全 P6-11 4-2
全 加器由兩個 半 加器與一個 閘 組合而成，而 減器 亦 練習
OR
可由兩個 半 減器與一個 閘 組合而成。
全 加器電路

全 減器電路

7483 、74283 的 IC 4 P6-14 1 、P6-18 3-3
編號 內 有四個 全 加器 串 接而成）。 皆為 位元的 加器 並 範例 練習
（

P6-15 2
並 加器與 加器的比較： 串 範例

並 加 器 串 加 器
電路屬於組合邏輯電路 電路屬於序向邏輯電路
n 位元的加法，須使用 n 個全加器 只須使用一個全加器與一個 D 型正反器

運算速度快，但電路較複雜 運算速度慢，但電路較簡單

使用並列輸入並列輸出的暫存器
使用串列移位暫存器