Page 25 - ePD035_數學學測模擬與歷屆試題含解析_課本PDF

模擬試題第 1 回 3

模擬試題 第 1 次練習 第 2 次練習 第 3 次練習 ◎ 每題可勾選難易度 a 1

7
2
第 1 回 分 分 分 易 中 難 ( 1 ) 5. 設 (2x + x ) 的展開式中 x 項的係數為 42 ¸則實數 a 的值為何﹖
5 16 3 4
(1) (2) (3) 1 (4) 5 2 (5) 3 2 。 易 中 難
2 2

a 7 7 2 m a n
x
2
解 (2x + ) ⇒ 每一項均為 C 2 ) ()
(
m
第壹部分：選擇題（占 65 分） x x
1 2mn m = 2
−= −1
一、單選題（占 35 分） x 項 ⇒  ⇒ 
+= 7
 mn  n = 5
共 7 次方
( 3 ) 1. 28 − 300 最接近以下哪個數？ 1 項係數 = C 2() () 5 = 42
7
2
a
x 2
(1) 1 (2) 2 (3) 3 (4) 4 (5) 5。 易 中 難 1 1 5 16
5
21 4⋅⋅a 5 = 42 a = ∴ a = = 。 【二項式定理】
2 5 2 2
解 28 − 300 = 28 − 2 75 = ( 25 − 3 )
2
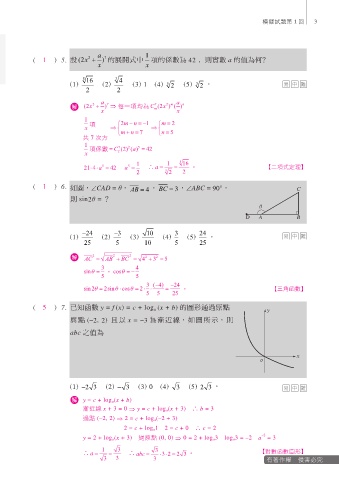
( 1 ) 6. 如圖，∠CAD = θ， ， BC = 3 ，∠ABC = 90°， C
=| 25 − 3 | =− 3 ≒ 5 – 1.732 ≒ 3.268 ≒ 3 ∴最接近 3。 【數與式】 AB = 4
5
則 sin2θ = ？
( 2 ) 2. 將編號 1 ～ 8 號的八顆球排成一列，其中偶數號球的編號由小到大排列次 θ
D A B
序不變（不一定相鄰）的機率為何？
1 1 1 1 1 −24 −3 10 3 24
(1) (2) (3) (4) (5) 。 易 中 難 (1) (2) (3) (4) (5) 。 易 中 難
6 24 120 720 5040 25 5 10 5 25
8! 解 2 2 2 2 2
將 4 顆偶數號球視為相同，方法數 = AC = AB + BC = 4 + 3 = 5
解 4!
4
8! sinθ = 3 ， cosθ =−
5
5
機率 = 4! = 1 = 1 。 【機率】 3 ( 4 ) − 24
−
8! 4! 24 sin2θ = 2 sinθ ⋅ cosθ =⋅ ⋅ = 。 【三角函數】
2
5 5 25
( 4 ) 3. 由常用對數表中查得 log 101.7 ≈ 0.2304 ¸ log 101.8 ≈ 0.2553。請問 10 –1.745 的
( 5 ) 7. 已知函數 y = f (x) = c + log a (x + b) 的圖形通過原點 y
值最接近下列哪一個選項﹖
與點 (–2, 2) 且以 x = –3 為漸近線，如圖所示，則
(1) 0.17 (2) 0.18 (3) 0.017 (4) 0.018 (5) 0.0017。 易 中 難
abc 之值為
解 設 a = 10 –1.745 loga = –1.745 = –2 + 0.255
5
=
.
.
−
.
0
 0 2553 02 50 00 3 x
 0
.
.
5
.
=
 025 − 0 2304 0024 6
0.0003 < 0.0246
–2
loga = –2 + 0.255 ≈ log10 + log1.8
–2
a ≒ 1.8 × 10 ≒ 0.018。 【指數對數】 (1) −23 (2) − 3 (3) 0 (4) 3 (5) 23 。 易 中 難
解 y = c + log a(x + b)
)
)( +
( 4 ) 4. 已知 –3 ≤ a ≤ 3，求 (3− aa 4 的最大值為何﹖ 漸近線 x + 3 = 0 ⇒ y = c + log a(x + 3) ∴ b = 3
過點 (–2, 2) ⇒ 2 = c + log a(–2 + 3)
7 11
(1) 0 (2) 6 (3) 23 (4) (5) 。 易 中 難 2 = c + log a1 2 = c + 0 ∴ c = 2
2 3
–2
y = 2 + log a(x + 3) 過原點 (0, 0) ⇒ 0 = 2 + log a3 log a3 = –2 a = 3
49 49 7
(3− aa ) 4 =−a 2 −+ 12 =−(a + ) + ≤ = 。 1 3
)( +
a
1 2
解 【多項式】 3 【對數函數圖形】
2 4 4 2 ∴ a = = ∴ abc = ⋅ ⋅= 23 。
32
3 3 3 有著作權 侵害必究
PD035_模擬試題.indd 3 1/4/2019 下午 06:44:12