Page 16 - ePD12109_數學B跨越講義_課本PDF

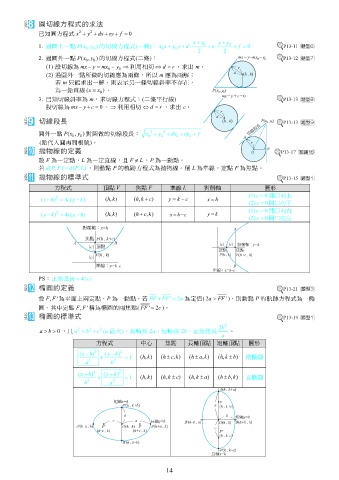
圓切線方程式的求法
已知圓方程式 x  2 y  2 dx ey   f  0

xx y  y
1. 過圓上一點 (, y 0 ) 的切線方程式(一條)： xx  y y d 0  e 0  f  0 P13-11
Px
0
0
0
2 2
2. 過圓外一點 (,Px y 0 ) 的切線方程式(二條)： P13-12
0
(1) 設切線為 mx  mx  y  利用相切  d  ，求出 m。
r
y
0
0
(2) 過圓外一點所做的切線應為兩條，所以 m 應為兩解；
若 m 只能求出一解，則表示另一條切線斜率不存在，
為一鉛直線 (x  x 0 ) 。
3. 已知切線斜率為 m，求切線方程式：(二條平行線) P13-13
設切線為 mx   。  利用相切  d  ，求出 c。
0
y c
r
切線段長 P13-13
2
Px
圓外一點 (, y 0 ) 對圓做的切線段長： x  y 0 2  dx  0 ey  0 f
0
0
(點代入圓再開根號)。
拋物線的定義 P13-17
設 F 為一定點，L 為一定直線，且 F  ，P 為一動點。
L
若 (, )  d ( , ) ，則動點 P 的軌跡方程式為拋物線。稱 L 為準線，定點 F 為焦點。
P
dP
L
F
拋物線的標準式 P13-15
方程式 頂點 V 焦點 F 準線 L 對稱軸 圖形
(1) c  開口向上
0





hk
)
)
(x h )  2 4 (y k (, ) (,hk c y  k c x h
c
0
(2) c  開口向下
(1) c  開口向右
0

k

k

hk
)
c
(y k )  2 4 (x h (, ) (hc , ) x hc y 


0
(2) c  開口向左

PS：正焦弦長  4| |
c
橢圓的定義 P13-21
設 ,' 為平面上兩定點，P 為一動點，若 PF  PF '  2a 為定值( 2a  FF ' )，則動點 P 的軌跡方程式為一橢
F
F
圓。其中定點 ,'F F 稱為橢圓的兩焦點( FF  2c )。
'
橢圓的標準式 P13-19
2b 2
a  0 ，且 a  2 b  2 c (a 最大)，長軸長 2a，短軸長 2b，正焦弦長 。
2
b
a
方程式 中心 焦點 長軸頂點 短軸頂點 圖形


(xh ) 2  (y k ) 2  1 (, ) (hc , ) (ha , ) (,hk b ) 橫橢圓



k
k
hk
a 2 b 2


(xh ) 2  (y k ) 2  1 (, ) (,hk c ) (,hk a ) (hb , ) 直橢圓



k
hk
b 2 a 2

14