Page 5 - ePD12109_數學B跨越講義_課本PDF

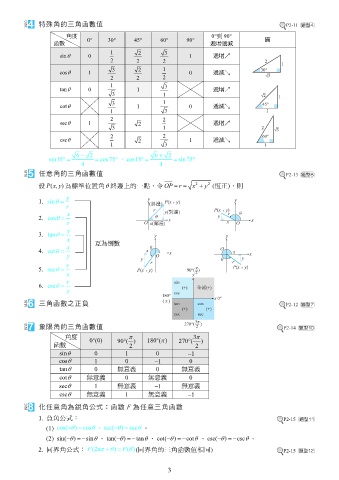
特殊角的三角函數值 P2-11
角度 0到 90 圖
函數 0 30 45 60 90 遞增遞減
1 2 3
sin 0 1 遞增↗
2 2 2
3 2 1
cos 1 0 遞減↘
2 2 2
1 3
tan 0 1 遞增↗
3 1
3 1
cot 1 0 遞減↘
1 3
2 2
sec 1 2 遞增↗
3 1
2 2
csc 2 1 遞減↘
1 3
6  2 6  2
sin15  cos75 ， cos15  sin75
4 4
任意角的三角函數值 P2-13

2
2
設 (, ) 為標準位置角 終邊上的一點，令 OP  x  y (恆正)，則
Px
r
y
y
1. sin 
r
x
2. cos 
r
y
3. tan 
x
x 互為倒數
4. cot 
y
r
5. sec 
x
r
6. csc 
y

三角函數之正負 P2-12

象限角的三角函數值 P2-14
角度 0(0)  180 ( ) 3




函數 90 ( ) 270 (  2 )
2
sin 0 1 0  1
cos 1 0  1 0
tan 0 無意義 0 無意義
cot 無意義 0 無意義 0
sec 1 無意義  1 無意義
csc 無意義 1 無意義  1
化任意角為銳角公式：函數 F 為任意三角函數

1. 負角公式： P2-15
(1) cos( ) cos 、 sec( ) sec 。





(2) sin(   )  sin 、 tan(   )  tan 、 cot(   cot 、 csc(   csc 。

)
)
2. 同界角公式： (2Fn   )  F ( )  (同界角的三角函數值相同) P2-15

3