Page 6 - ePD12109_數學B跨越講義_課本PDF

3. 化銳角公式： P2-15

n
 n   F () 當為偶數  n 
F (  )   ，±視原函數 F  (  )  的象限來判斷。

n
2  coF () 當為奇數 2
三角函數的基本關係
1. 餘角關係：(正  餘) P2-19
sin(90  ) cos tan(90  ) cot sec(90  ) csc




cos(90  ) sin cot(90 )   tan csc(90  ) sec
2. 倒數關係： P2-19
sin   csc   1 cos   sec   1 tan  cot  1
1 1 1
csc  sec  cot 
sin cos tan
3. 平方關係： P2-21
2
sin   cos  2  1 sin  2  1 cos   2  cos  2  1 sin   2
tan  2 1  2 sec   2  sec  2  tan  2  1 cot  2 1  2 csc   2  csc  2  cot  2  1
sin cos
4. 商數關係： tan  ； cot  P2-19
cos sin

5. 三角函數基本關係的延伸，常用於求值： P2-20
1


(1) (sin   cos )  2 1 2sin cos      1 sin 2 (2) tan   cot  
sin cos

3


(3) sin   3 cos  3 (sin    cos )  3sin cos (sin    cos )





sin   或 3 cos  3 (sin    cos )(1 sin cos )
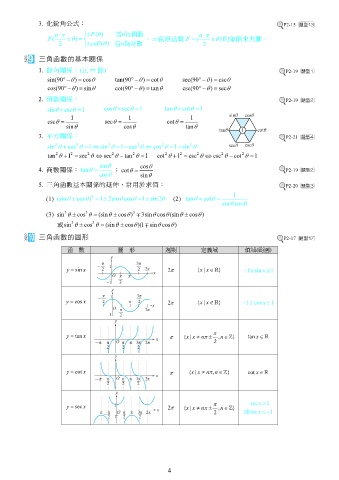
三角函數的圖形 P2-17
函 數 圖 形 週期 定義域 值域(範圍)
y  sin x 2 {|xx   1
}
1sin x 

y  cos x 2 {|xx   1
}
1cos x 

y  tan x  {|xx  n   ,n  } tan x 
2

y  cot x  {|xx  n ,n cot x  
}

y  sec x 2 {|xx  n   ,n  } sec x  1
2 或 sec x  1

4