Page 15 - eAC00220_基本電學II_課本PDF

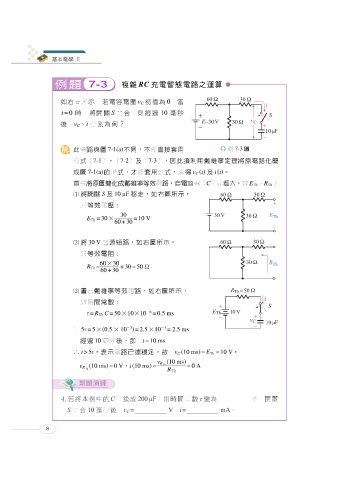
7-3 複雜 RC 充電暫態電路之運算

v C
如右圖所示，若電容電壓 初值為 0 ，當
t =0 S 10
時，將開關 閉合，則經過 毫秒
、i
v C
後， 分別為何？

7-1(a) 不同，不能直接套用 例 7-3 圖
此電路與圖

公式 （7-1 ）、（ 7-2 ） 及 （7-3 ），因此須利用戴維寧定理將原電路化簡
7-1(a) v C t 及 i t
成圖 的形式，才能套用公式，求得 。
（C E 、R
容
首先將原 圖簡化成戴維寧等效電路，自電 器 ）端看入，求 ：
S 及 10 F
將開關 移走，如右圖所示，
求等效電壓：
30
E =30 =10 V
60 + 30
×
將 30 V 電源短路，如右圖所示，

求等效電阻：
60 ×30
R = +30=50
60 + 30

畫出戴維寧等效電路，如右圖所示，

求時間常數：
6
= R C =50 ×10 ×10 = 0.5 ms
∵ 5 =5 × 0.5 × 10 3 = 2.5 ×10 = 2.5 ms
3
10 t =10 ms
經過 毫秒後，即
∴ t >5 ，表示電路已達穩定，故 v C 10 = E =10 V ，
10
v R
10 =0 V ，i 10 = =0 A
v R
R

C
若將本例中的 值換成 200 F ，則時間常數 變為 秒，開關
S 閉合 10 毫秒後， v C = V ，i= mA 。

8