Page 17 - ePD12308_升科大四技數學 B 最佳方略含解析本_課本PDF

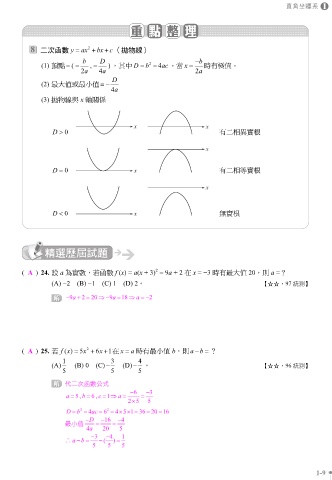
二次函數 y  ax  2 bx c （拋物線）

b D  b
(1) 頂點 ( ,  ) ，其中 D  b  2 4ac 。當 x  時有極值。
2a 4a 2a
D
(2) 最大值或最小值 
4a

(3) 拋物線與 x 軸關係

D  0 有二相異實根

D  0 有二相等實根

D  0 無實根

2
( A ) 24. 設 a 為實數，若函數 f (x) = a(x + 3)  9a + 2 在 x = −3 時有最大值 20，則 a =？
(A) −2 (B) −1 (C) 1 (D) 2。 【☆☆，97 統測】

 9a  2 20   9a  18  a   2


( A ) 25. 若 ()  f x 5x  2 6x  1在 x  時有最小值 b，則 ab  ？

a
1 3 4
(A) (B) 0 (C)  (D)  。 【☆☆，96 統測】
5 5 5
代二次函數公式
 6  3
a  5, b  6 , c  1  a  

25 5
Db  2 4ac  6  2 4 5 1 36 20 16






 D  16  4
最小值  
4a 20 5
 3  4 1

∴ ab  ( ) 
5 5 5

1-9